यंग का द्वि स्लिट प्रयोग (Young’s Double slit Experiment)
Table of Contents
यंग का द्वि स्लिट प्रयोग –
सन् 1802 में अंग्रेज वैज्ञानिक थामस यंग ने दो तरंगों से उत्पन्न व्यतिकरण की घटना को प्रदर्शित करने के लिए एक प्रयोग कहते हैं।
इसमें S एक संकीर्ण स्लिट है जो एकवर्णी प्रकाश स्त्रोत से प्रकाशित होता है।
इससे कुछ ही दूरी पर एक गत्ते में एक दूसरे के समान्तर तथा बिल्कुल निकट दो अन्य स्लिटें S₁ और S₂ बने होते हैं।
ये दोनों स्लिटें कला सम्बद्ध स्त्रोत की तरह कार्य करते हैं।
इनसे कुछ ही दूरी पर एक पर्दा XY रखा होता है , जिस पर व्यतिकरण प्रतिरूप प्राप्त होता है।
जब स्लिट S को एकवर्णी (Monochromatic) प्रकाश स्त्रोत से प्रकाशित किया जाता है ,
तो निम्नलिखित प्रक्षेण प्राप्त होते हैं –
1. पर्दा XY पर एकान्तर क्रम में चमकीली और काली पट्टियां दिखाई देती हैं इन्हें दीप्त और अदीप्त फ्रिंज कहते हैं।
एकान्तर क्रम में दीप्त और अदीप्त फ्रिंजों के समूह को व्यतिकरण प्रतिरूप कहते हैं।
2. प्रत्येक दीप्त फ्रिंज की तीव्रता एकसमान (अधिकतम ) होती है।
3. प्रत्येक अदीप्त फ्रिंज की तीव्रता भी एकसमान (लगभग शून्य) होती है।
4. समस्त दीप्त और अदीप्त फ्रिंजों की चौड़ाई एकसमान होती है।
तरंग सिद्धांत से व्यतिकरण की व्याख्या :-
हाइगन के तरंग सिद्धांत के अनुसार प्रकाश स्त्रोत S से प्रकाश तरंग के रूप में अर्थात् श्रृंग और गर्त के रूप में आगे बढ़ता है।
इन्हें चित्र 2 में क्रमशः बिन्दुदार और सतत् रेखाओं के चापों द्वारा प्रदर्शित किया जाता है।
जब प्रकाश की यह तरंग S₁ और S₂ पर पहुँचती है तो ये बिन्दु द्वितीयक तरंगिकाओं के स्त्रोत बनकर माध्यम में आगे की ओर श्रृंग और गर्त के रूप में तरंगें प्रेषित करते हैं।
ये तरंगें माध्यम में एक दूसरे पर अध्यारोपित होती है।
ऐसे बिन्दु जहाँ श्रृंग , श्रृंग पर तथा गर्त , गर्त पर अध्यारोपित होते हैं , अधिक तीव्रता का निर्माण करते हैं। यह संपोषी व्यतिकरण की स्थिति होती है।
ऐसे बिन्दु जहाँ श्रृंग , गर्त पर या गर्त , श्रृंग पर अध्यारोपित होते हैं , न्यूनतम तीव्रता के क्षेत्र या अन्धकार के क्षेत्र का निर्माण करते हैं।
यह विनाशी व्यतिकरण की स्थिति होती है।
चित्र 2 में संपोषी व्यतिकरण को ×(क्रॉस) द्वारा और विनाशी व्यतिकरण को ● (डॉट) द्वारा प्रदर्शित किया गया है।
पर्दे XY पर अधिकतम तीव्रता व अन्धकार के क्षेत्र क्रमशः B और D द्वारा प्रदर्शित किये गये हैं।
चूँकि स्त्रोत S₁ और S₂ स्लिट हैं , पर्दे पर भी B और D स्लिट के आकार के बनते हैं।
इन्हें फ्रिंज कहते हैं।
B दीप्त फ्रिंजों को तथा D अदीप्त फ्रिंजों को प्रदर्शित करते हैं।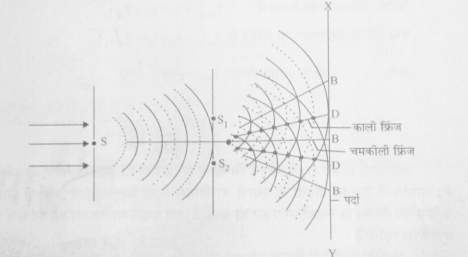
दो क्रमागत दीप्त फ्रिंजों या अदीप्त फ्रिंजों के बीच की दूरी सदैव समान होती है , इसे फ्रिंज चौड़ाई कहते हैं।
यदि दोनों स्लिटों के बीच की दूरी d तथा S₁ या S₂ की पर्दे से दूरी D हो , तो फ्रिंज चौड़ाई β = λD/d,
जहाँ λ प्रकाश का तरंगदैर्ध्य है।
चित्र 3 में अधिकतम तीव्रता और न्यूनतम तीव्रता की स्थितियों को प्रदर्शित किया गया है।
व्यतिकरण की घटना ऊर्जा संरक्षण के नियम के अनुकूल है –
मानलो दो कला सम्बद्ध स्त्रोतों से उत्सर्जित प्रकाश तरंगों की तीव्रता क्रमशः I₁ व I₂ हैं।
यदि दोनों तरंगें व्यतिकरण न करें , तो पर्दे के किसी बिन्दु पर परिणामी तीव्रता
I = I₁ +I₂ ………(1)
किन्तु यदि दोनों तरंगें व्यतिकरण करती हों तो संपोषी और विनाशी व्यतिकरण के कारण तीव्रता अधिकतम और न्यूनतम होगी।
संपोषी व्यतिकरण की स्थिति में ,
Imax = I₁ + I₂ + 2√I₁I₂
तथा विनाशी व्यतिकरण की स्थिति में ,
Imix = I₁ + I₂ – 2√I₁I₂
अतः पर्दे पर औसत तीव्रता
Iavr =( Imax + Imin )/2
= I₁+I₂ +2√I₁I₂ + I₁ + I₂ -2√I₁I₂
Iavr = I₁ + I₂……(2)
समीकरण (1) और (2) से स्पष्ट है कि
पर्दे के प्रत्येक बिन्दु पर व्यतिकारी तरंगों की कुल ऊर्जा नियत रहती है।
वास्तव में , न्यूनतम तीव्रता के स्थानों पर जितनी ऊर्जा विलुप्त होती है उतनी ही अतिरिक्त ऊर्जा अधिकतम तीव्रता के स्थानों पर प्रकट हो जाती है।
इस प्रकार व्यतिकरण की घटना में ऊर्जा का केवल पुनर्वितरण होता है।
फ्रिंज चौड़ाई की निर्भरता
फ्रिंज चौड़ाई निम्न कारकों पर निर्भर करती है –
1. प्रकाश के तरंगदैर्घ्य पर –
फ्रिंज चौड़ाई β प्रकाश के तरंगदैर्घ्य के अनुक्रमानुपाती होती है।
अतः अधिक तरंगदैर्घ्य के प्रकाश के लिए फ्रिन्ज चौड़ाई अधिक तथा कम तरंगदैर्ध्य के प्रकाश के लिए फ्रिन्ज चौड़ाई कम होती है।
चूँकि लाल रंग का तरंगदैर्घ्य बैगनी रंग के तरंगदैर्घ्य से अधिक होता है ,
अतः लाल रंग के प्रकाश के लिए फ्रिन्ज चौड़ाई अधिक तथा बैंगनी रंग के प्रकाश के लिए फ्रिन्ज चौड़ाई कम होती है।
2. कला सम्बद्ध स्त्रोतों के बीच की दूरी पर –
फ्रिन्ज चौड़ाई β कलासम्बद्ध स्त्रोतों के बीच की दूरी d के व्युत्क्रमानुपाती होती है।
इस प्रकार कलासम्बद्ध स्त्रोतों के निकट होने पर फ्रिन्ज चौड़ाई अधिक तथा दूर होने पर फ्रिन्ज चौड़ाई कम होती है।
3. कलासम्बद्ध स्त्रोतों से पर्दे की दूरी पर –
फ्रिन्ज चौड़ाई β दोनों कलासम्बद्ध स्त्रोतों से पर्दे की दूरी D के अनुक्रमानुपाती होती है।
इस प्रकार दूरी D अधिक होने पर फ्रिन्ज चौड़ाई अधिक और दूरी D कम होने पर फ्रिन्ज चौड़ाई कम होती है।
प्रकाश का तरंगदैर्घ्य ज्ञात करना –
फ्रिन्ज चौड़ाई β = λD/d या λ=βd/D, इस रूप में यदि β, D और d के मान ज्ञात हों तो प्रकाश का तरंगदैर्घ्य λ ज्ञात किया जा सकता है।
चूँकि λ का मान नियत रहता है तथा D का मान अधिक बढ़ाया नहीं जा सकता , दोनों कलासम्बद्ध स्त्रोतों के बीच की दूरी d को कम से कम रखा जाना चाहिए।
विभिन्न परिस्थितियों में व्यतिकरण प्रतिरूप में होने वाले परिवर्तन –
1. एकवर्णी प्रकाश स्त्रोत के स्थान पर श्वेत प्रकाश स्त्रोत का उपयोग करने पर –
श्वेत प्रकाश सात रंगों से बना होता है।
जब एकवर्णी प्रकाश स्त्रोत श्वेत प्रकाश स्त्रोत से प्रतिस्थापित कर दिया जाता है तो केन्द्रीय चमकीली फ्रिन्ज की स्थिति सभी रंगों के लिए एक ही होती है।
अतः केन्द्रीय फ्रिन्ज श्वेत होती है।
अन्य चमकीली फ्रिंजों की स्थिति भिन्न भिन्न रंगों के लिए भिन्न भिन्न होती है।
अतः अन्य फ्रिंजे रंगीन बनती हैं।
बैंगनी रंग का तरंगदैर्घ्य λ सबसे कम तथा लाल रंग का तरंगदैर्घ्य सबसे अधिक होता है।
अतः बैंगनी रंग की फ्रिन्ज की कोणीय चौड़ाई सबसे कम तथा लाल रंग की फ्रिन्ज की कोणीय चौड़ाई सबसे अधिक होती है।
अतः प्रत्येक फ्रिन्ज का वह किनारा जो केन्द्रीय फ्रिन्ज की ओर होता है , बैंगनी तथा दूसरा किनारा लाल रंग का दिखाई देता है।
2. प्रयोग , वायु के स्थान पर जल में करने पर –
हम जानते हैं कि ₐμw = λₐ / λw
चूँकि ₐμw>1 ,
चूँकि λw< λₐ
अर्थात् जल में प्रकाश का तरंगदैर्घ्य वायु की तुलना में कम होता है।
अब यंग के द्वि स्लिट प्रयोग से ,
β =λD/d
यदि D और d नियत हो , तो
βₐ/βw = λₐ/λw
चूँकि λw<λₐ , इसलिए βw<βₐ
अर्थात् जल में फ्रिन्ज चौड़ाई वायु में फ्रिन्ज चौड़ाई की तुलना में कम हो जाती है।
पुनः μ = λₐ / λw
अतः उपर्युक्त समीकरण से ,
μ =βₐ/βw
या βw = βₐ/ μ
3. एक स्लिट को बन्द कर देने पर –
ऐसा करने से व्यतिकरण प्रतिरूप के स्थान पर विवर्तन प्रतिरूप प्राप्त होगा।
फ्रिंजे समदूरस्थ नहीं होंगी तथा इनकी तीव्रता क्रमशः घटती जायेंगी( यदि स्लिट का आकार प्रकाश के तरंगदैर्घ्य की कोटि का है। )
4. एक स्लिट को नीले तथा दूसरे स्लिट को लाल सेलोफेन कागज से ढँक देने पर –
व्यतिकरण प्रतिरूप प्राप्त नहीं होगा , क्योंकि दोनों तरंगों का तरंगदैर्ध्य अलग अलग होगा।
5., जब स्लिटों के बीच की दूरी d <λ –
इस स्थिति में β > D अतः व्यतिकरण प्रतिकरण प्रतिरूप प्राप्त नहीं होगा।
6. एक स्लिट पूर्ण रूप से तथा दूसरा स्लिट आंशिक रूप से खुला है-
भिन्न भिन्न आयामों की तरंगों द्वारा व्यतिकरण होगा , किन्तु विपर्यास (Contrast) अच्छा नहीं होगा।
7. एक स्लिट को सेलोफेन कागज से ढँकने पर –
दीप्त फ्रिन्ज कम दीप्त तथा अदीप्त फ्रिन्ज कम अदीप्त होगी।
यंग के द्वि-स्लिट प्रयोग का महत्व (Importance of Young’s Double Slit Experiment ) –
यंग के द्वि-स्लिट प्रयोग के मुख्यतः दो महत्व है –
(1). यह प्रकाश के व्यतिकरण को प्रदर्शित करने वाला पहला प्रयोग था।
(2). इस प्रयोग से यह सिद्ध होता है कि प्रकाश तरंग के रूप में संचरित होता है।
केवल प्रकाश का तरंग सिद्धांत ही व्यतिकरण की संतोषप्रद व्याख्या कर सकता है।
यंग ने अपने प्रयोग में सूर्य प्रकाश का तथा स्लिट के स्थान पर सूची छिद्र (Pinhole) का प्रयोग किया था।
चूंकि सूर्य प्रकाश सात रंगो से निर्मित होता है , दीप्त फ्रिंजें रंगीन एवं अस्पष्ट थीं तथा उनकी संख्या बहुत ही कम थी।
सूर्य प्रकाश के स्थान पर एकवर्णी प्रकाश-स्त्रोत प्रयुक्त करने पर स्पष्ट व्यतिकरण-प्रतिरूप प्राप्त होता है।
पतली फिल्मों के रंग ( Colours of Thin Films)
Varsha Ritu Mein vibhinn motor वाहनों se टपकी Tel ki bunde Sadak per Patali film ke roop Mein bikhar Jaati Hai.
Surya ke Prakash Mein yah film vibhinn rangon ki Dikhai Deti Hai .
Is Tarah Jal Ki satah par Tel ki boondan se bani Patali film bhi Rangeen Dikhai Deti Hai .
sabun ke Rangeen Bulbulay bhi Surya ke Prakash Mein Rangeen Dikhai Dete Hain.
ine Sab Ka Karan Prakash Ka vyatikaran Hai.
Jab Surya ka Prakash Kisi Patali film (Jiski मोटाई Prakash के तरंगदैर्घ्य की Koti ki Hoti Hai) per आपतित hota hai ,
to uska Kuchh Bhag film ke upari पृष्ठ se paraavartit ho jata hai tatha शेष भाग उसके andar Pravesh Karke Nichle पृष्ठ se paraavartit hota hai .
donon पृष्ठों se paraavartit in Prakash rangon Mein व्यतिकरण hota hai.
chuki swet Prakash 7 rangon Se Milkar banaa Hota Hai , paraavartit rangon ke vyatikaran Ke Karan film Rangeen Dikhai Deti Hai.
गणितीय गणना ke Aadhar per Siddh Kiya jata hai ki vyatikaran tarangon ke Madhya
पथान्तर ∆ = 2μt cos r होता है ,
जहाँ μ = फिल्म का अपवर्तनांक ,
t = फिल्म की मोटाई तथा r =अपवर्तन कोण।
yadi आपतन कोण ka man Badalta Hai ,To apvartan kon r ka man bhi badlega.
फलस्वरूप pathantar ∆ bhi Badal Jayega.
spasht hai ki bhinn bhinn दिशाओं Se Dekhne per film bhinn bhinn Rang ki Dikhai Degi.
film Ki मोटाई t badalne per bhi pathantar ∆ Badal Jata Hai .
atah film ki motai badalne per vibhinn vibhinn rangon ki Dikhai Deti Hai.
परावर्तित प्रकाश में बहुत ही पतली फिल्म अदीप्त दिखाई पड़ती है –
Iska Karan yah Hai Ki यदि फिल्म की motai t bahut hi kam hai arthat t<<λ , to paraavartit Prakash Mein pathantar ∆ = 2μt cos r lagbhag शून्य Hoga .
अतः Prakash ke sabhi तरंगदैर्घ्य के लिए विनाशी व्यतिकरण ki शर्तें santusht ho jaayengi .
atah paraavartit Prakash Mein film adeept Dikhai padegi.
Parvati Prakash Mein Moti फिल्म bhi Rangeen Dikhai Nahin Degi , अपितु Ek Saman swet prakash se prakashit Dikhai deti hai.
iska Karan kya hai ki yadi फिल्म ki motor bahut Adhik Hai , To पथान्तर अधिक ho jata hai.
अतः श्वेत Prakash के Kuch तरंगदैर्घ्य संपोषी व्यतिकरण tatha Kuchh तरंगदैर्घ्य vinashi vyatikaran utpann karte hain .
फलस्वरूप film Rangeen Dikhai Na De kar Ek Saman swet prakash se prakashit Dikhai Deti Hai.
film kiमोटाई t badalne per bhi pathantar ∆ Badal Jaate Hain .
अतः film ki motai badalne per vah bhinn bhinn rangon ki Dikhai Degi .
yah bhi उल्लेखनीय Hai Ki यदि film Ki मोटाई bahut hi kam ho to vah Kali Dikhai Deti Hai , किन्तु yadi uski मोटाई अधिक है , तो Rangeen dekhne ki बजाय ek Saman swet Prakash Dikhai Deti Hai .
यंग का द्वि स्लिट प्रयोग
सूक्ष्मदर्शी (Microscope) किसे कहते हैं ?
तरंगाग्र (Wavefront) किसे कहते हैं ?
